数学五年级上册知识点总结

2024-05-03 05:29:18

数学五年级上册知识点总结

欢迎大家加入这个数学五年级上册知识点总结问题集合的讨论。我将充分利用我的知识和智慧，为每个问题提供深入而细致的回答，希望这能够满足大家的好奇心并促进思考。

1.五年级上册数学重要知识点总结

2.人教版小学数学五年级上册知识点有哪些

3.谁可以帮我总结一下苏教版数学五年级上册的所有公式

数学五年级上册知识点总结

五年级上册数学重要知识点总结

有很多同学在复习五年级上册数学知识点时，因为没有系统的总结而头疼。下面是由我为大家整理的“五年级上册数学重要知识点总结”，仅供参考，欢迎大家阅读本文。

　一、小数乘法

　1、小数乘整数：意义——求几个相同加数的和的简便运算。

　如：1.5×3表示1.5的3倍是多少或3个1.5是多少。

　计算方法：先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

　2、小数乘小数：意义——就是求这个数的几分之几是多少。

　如：1.5×0.8(整数部分是0)就是求1.5的十分之八是多少。

　1.5×1.8(整数部分不是0)就是求1.5的1.8倍是多少。

　计算方法：先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

　注意：计算结果中，小数部分末尾的0要去掉，把小数化简;小数部分位数不够时，要用0占位。

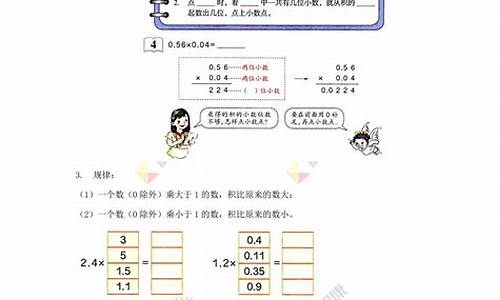
　3、规律：一个数(0除外)乘大于1的数，积比原来的数大;一个数(0除外)乘小于1的数，积比原来的数小。

　4、求近似数的方法一般有三种：

　(1)四舍五入法;(2)进一法;(3)去尾法

　5、计算钱数，保留两位小数，表示计算到分。保留一位小数，表示计算到角。

　6、小数四则运算顺序跟整数是一样的。

　7、运算定律和性质：

　加法：加法交换律：a+b=b+a　　加法结合律:(a+b)+c=a+(b+c)

　乘法：乘法交换律：a×b=b×a

　乘法结合律：(a×b)×c=a×(b×c)见2.5找4或0.4，见1.25找8或0.8

　乘法分配律：(a+b)×c=a×c+b×c或a×c+b×c=(a+b)×c(b=1时，省略b)

　变式：(a-b)×c=a×c-b×c或a×c-b×c=(a-b)×c

　减法：减法性质：a-b-c=a-(b+c)

　除法：除法性质：a÷b÷c=a÷(b×c)

　二、多边形的面积

　1、公式

　长方形：周长=(长+宽)×2;　　面积=长×宽;

　正方形：周长=边长×4;　　面积=边长×边长;

　平行四边形：面积=底×高;

　三角形：面积=底×高÷2;

　梯形：面积=(上底+下底)×高÷2;

　2、单位换算的方法

　大化小，乘进率;小化大，除以进率。

　3、常用单位间的进率

　1千米=1000米1米=10分米

　1分米=10厘米1厘米=10毫米

　1平方千米=100公顷1公顷=10000平方米

　1平方米=100平方分米1平方分米=100平方厘米

　4、图形之间的关系

　(1)、平行四边形可以转化成一个长方形;两个完全相同的三角形可以拼成一个平行四边形。两个完全相同的梯形可以拼成一个平行四边形。

　(2)、等底等高的平行四边形面积相等;等底等高的三角形面积相等。

　(3)、等底等高的平行四边形面积是三角形面积的2倍。如果一个三角形和一个平行四边形等面积，等底，则三角形的高是平行四边形的2倍。如果一个三角形和一个平行四边形等面积，等高，则三角形的底是平行四边形的2倍。

　(4)、把长方形框架拉成平行四边形，周长不变，面积变小了。

　5、求组合图形面积的方法

　(1)仔细观察，确定组合图形可以分割或添补成哪些可以计算面积的基本图形。

　(2)找到计算这些基本图形的面积所需要的数据。

　(3)分别计算这些基本图形的面积，然后再相加或相减。

人教版小学数学五年级上册知识点有哪些

一、1.小数除法→除数是整数的除法

2.利用积的变化规律，观察小数的位数。

3.规律的应用。

一个数（0除外）乘大于 1的数，积比原数大。

一个数（0除外）乘小于 1的数，积比原数小。

一个数（0除外）除以大于 1的数，商比原数小。

一个数（0除外）除以小于 1的数，商比原数大。

4.用字母表示数。（注意：数与字母相乘，乘号省略）

5.循环小数（易算错，精确到百分位=保留两位小数）

6单位换算（ 1公顷=10000平方米，时间单位之间的进率是60。45分=0.75时）

7.三角形面积公式（求底）。

8.长方形周长与面积的应用。（公式及单位）

已知周长和长，先求宽36÷2-10=8（厘米）

再求出面积，10×8=80（平方厘米）。根据增加后的长10+6=16（厘米），求出宽80÷16=5（厘米）。

9.长方形与三角形的关系

10.可能性

11.平行四边形与梯形的关系。

二、 1.与填空2知识点相同，换种说法。

2.循环小数是无限小数。

3.小数乘整数与整数乘法的意义相同

小数乘小数与整数乘法意义不同

4. 三角形是等底等高的平行四边形面积的一半。

5. 完全相同（形状、大小）的三角形能拼成一个平行四边形。

面积相等形状不一定相同。

三、1.用字母表示数

2.用数对确定位置。

3.可运用填空2知识点

注意选项A和选项D都大于a，可举例比较。如:假设a＝1，则A选项为1.02，而D为1÷0.02=50

4.考查对小数意义的理解

5.可运用被除数、除数、商与余数之间的关系。商×除数+余数=被除数。

四、1.注意： 0.1÷0.01+8.5

计算时0.1÷0.01错看成1÷0.01

2.列竖式计算中三道题都需要“精确到十分位”，即保留一位小数。

3.运用积的变化规律及乘法分配律。17.6×84+176×1.6

可将17.6×84转化为176×8.4

或将176×1.6转化为17.6×16

4.解方程的题目

注意解题方法及技巧。

形如ax+b=c的方程，把ax看作一个整体

形如a（x+b）=c的方程，把小括号里的算式看作一个整体。

五、画图题：

1.标出数据2.计算验证

方法一：

阴影部分面积=梯形面积-空白三角形面积

方法二：阴影部分面积=两个阴影三角形面积之和=底60厘米高30厘米的三角形面积

六、1.考查植树问题

注意关键词：两端都栽、走廊两侧

2 . 考查找数量关系及列方程解决问题

等量关系：

三年级植树棵树×2-16=五年级植树棵树

3.相遇问题及列方程

等量关系：

甲的速度×时间+乙的速度×时间=总路程

4.考查多边形面积的应用

由梯形面积公式得出总面积

注意：每平方米所用的油漆量×总面积=共需油漆量

5.分段计费问题

注意：不足1千米按1千米计算

因此，8.2千米按9千米计算，即8.2千米≈9千米。

谁可以帮我总结一下苏教版数学五年级上册的所有公式

小学五年级数学上册复习教学知识点归纳总结

第一单元小数乘法

1、小数乘整数（P2、3）：意义——求几个相同加数的和的简便运算.

如：1.5×3表示1.5的3倍是多少或3个1.5的和的简便运算.

计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数,就从积的右边起数出几位点上小数点.

2、小数乘小数（P4、5）：意义——就是求这个数的几分之几是多少.

如：1.5×0.8就是求1.5的十分之八是多少.

1.5×1.8就是求1.5的1.8倍是多少.

计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数,就从积的右边起数出几位点上小数点.

注意：计算结果中,小数部分末尾的0要去掉,把小数化简；小数部分位数不够时,要用0占位.

3、规律（1）（P9）：一个数（0除外）乘大于1的数,积比原来的数大；

一个数（0除外）乘小于1的数,积比原来的数小.

4、求近似数的方法一般有三种：（P10）

⑴四舍五入法；⑵进一法；⑶去尾法

5、计算钱数,保留两位小数,表示计算到分.保留一位小数,表示计算到角.

6、（P11）小数四则运算顺序跟整数是一样的.

7、运算定律和性质：

加法：加法交换律：a+b=b+a 加法结合律:(a+b)+c=a+(b+c)

减法：减法性质：a-b-c=a-(b+c) a-(b-c)=a-b+c

乘法：乘法交换律：a×b=b×a

乘法结合律：(a×b)×c=a×(b×c)

乘法分配律：(a+b)×c=a×c+b×c(a-b)×c=a×c-b×c

除法：除法性质：a÷b÷c=a÷(b×c)

第二单元小数除法

8、小数除法的意义：已知两个因数的积与其中的一个因数,求另一个因数的运算.

如：0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算.

9、小数除以整数的计算方法（P16）：小数除以整数,按整数除法的方法去除.,商的小数点要和被除数的小数点对齐.整数部分不够除,商0,点上小数点.如果有余数,要添0再除.

10、（P21）除数是小数的除法的计算方法：先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算.

注意：如果被除数的位数不够,在被除数的末尾用0补足.

11、(P23)在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数.

12、(P24、25)除法中的变化规律：①商不变性质：被除数和除数同时扩大或缩小相同的倍数（0除外）,商不变.②除数不变,被除数扩大,商随着扩大.③被除数不变,除数缩小,商扩大.

13、(P28)循环小数：一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数.

循环节：一个循环小数的小数部分,依次不断重复出现的数字.如6.3232……的循环节是32.

14、小数部分的位数是有限的小数,叫做有限小数.小数部分的位数是无限的小数,叫做无限小数.

第三单元观察物体

15、从不同的角度观察物体,看到的形状可能是不同的；观察长方体或正方体时,从固定位置最多能看到三个面.

第四单元简易方程

16、（P45）在含有字母的式子里,字母中间的乘号可以记作“ ”,也可以省略不写.

加号、减号除号以及数与数之间的乘号不能省略.

17、a×a可以写作a a或a ,a 读作a的平方. 2a表示a+a

18、方程：含有未知数的等式称为方程.

使方程左右两边相等的未知数的值,叫做方程的解.

求方程的解的过程叫做解方程.

19、解方程原理：天平平衡.

等式左右两边同时加、减、乘、除相同的数（0除外）,等式依然成立.

20、10个数量关系式：加法：和=加数+加数一个加数=和-两一个加数

减法：差=被减数-减数被减数=差+减数减数=被减数-差

乘法：积=因数×因数一个因数=积÷另一个因数

除法：商=被除数÷除数被除数=商×除数除数=被除数÷商

21、所有的方程都是等式,但等式不一定都是等式.

22、方程的检验过程：方程左边=……

23、方程的解是一个数；

解方程式一个计算过程.=方程右边

所以,X=…是方程的解.

第五单元多边形的面积

23、公式：长方形：周长=(长+宽)×2——长=周长÷2-宽；宽=周长÷2-长字母公式：C=(a+b)×2

面积=长×宽

五年级上册数学知识点总结

第一单元：负数的初步认识

正负数是表示相反意义的数。0既不是正数也不是负数，正数都大于0，负数都小于0。

0比任何的负数都大。

第二单元：多边形的面积计算

1.平行四边形的面积 = 底×高字母公式： S = a h 2.三角形的面积 = 底×高÷2 字母公式： S = a h÷2 3.梯形的面积 = （上底+下底）×高÷2 字母公式： S = (a + b ) h÷2 4.一个平行四边形能分割成两个完全相同的三角形；两个完全相同的三角形能拼成一个平行四边形。

5.一个平行四边形能分割成两个完全相同的梯形；两个完全相同的梯形可能拼成一个平行四边形。

6.等底等高的三角形的面积相等；一个三角形的面积是与它等底等高的平行四边形面积的一半。

7.长度单位：毫米（mm）厘米（cm）分米（dm）米（m）千米（km）

进率： 10 10 10 1000 8.面积单位：

测量和计算土地面积，通常用公顷作单位。边长是100米的正方形土地，面积是1公顷（hm）。

测量和计算大面积土地，通常用平方千米作单位。边长是1000米的正方形土地，面积是1平方千米（km）。1平方千米（km）＝1000000平方米（m2）

面积单位：平方厘米（cm2）平方分米（dm2）平方米（m2）公顷（hm2）平方千米（km2）

进率： 100 100 10000 100 9.重量单位：克（g）千克（kg）吨（t）

进率： 1000 1000

10.容积单位：毫升（mL）升（L）

进率 1000

第三单元：小数的意义和性质

1.分母是10、100、1000?的分数都可以用小数表示，一位小数表示十分之几、两位小数表示百分之几、三位小数表示千分之几?

2.小数点右边第一位是十分位，计数单位是十分之一（0.1）；小数点右边第二位是百分位，计数单位是百分之一（0.01）；小数点右边第三位是千分位，计数单位是千分之一（0.001）?；每相邻的两个计数单位之间的进率都是10。

4.小数的末尾添上0或者去掉0，小数的大小不变，这是小数的性质。根据小数的性质，通常可以去掉小数末尾的0把小数化简。

void function(e,t){for(var n=t.getElementsByTagName("img"),a=+new Date,i=[],o=function(){this.removeEventListener&&this.removeEventListener("load",o,!1),i.push({img:this,time:+new Date})},s=0;s< n.length;s++)!function(){var e=n[s];e.addEventListener?!e.complete&&e.addEventListener("load",o,!1):e.attachEvent&&e.attachEvent("onreadystatechange",function(){"complete"==e.readyState&&o.call(e,o)})}();alog("speed.set",{fsItems:i,fs:a})}(window,document);

5.把一个数改写成用“万”作单位的数，只要在这个数万位（从个位向左数第5位）后右下角点上小数点，再在数的末尾添写“万”字。把一个数改写成用“亿”作单位的数，只要在这个数亿位（个位向左第9位）后右下角点上小数点，再在数的末尾添写“亿”字。小数部分末尾的0一般省略不写。

第四单元：小数加减法

小数加减法的计算方法：相同数位对齐；小数点对齐；和里的小数点要和加数里的小数点对齐；差里的小数点要和被减数、减数的小数点对齐。从最低位算起：各位满十要进一；不够减时要向前一位退1作10再减。

第五单元：小数乘法和除法

1. 小数乘以整数的意义（小数乘以整数和整数乘法的意义相同，都是求

几个相同加数和的简便运算）例如：0.3×4（就是求4个0.3的和是多少？或者是0.3的4倍是多少？）

2. 小数乘整数的计算方法是用整数乘法进行计算求出积，然后看因数里

有几位小数就从积的个位起向左数几位点上小数点。 3. 整数乘以小数（意义是求这个数的十分之几、百分之几、千分之几?

是多少？）

4. 整数乘小数的计算方法是用整数乘法的计算方法求出积，然后看因数

中有几位小数再从积的个位起向左数几位点上小数点。

5. 小数乘小数的计算方法是用整数乘法进行计算求出积，然后看因数中

一共有几位小数，就从积的个位起向左数几位点上小数点；数位不够时一定用“0”来补足数位。 6.一个小数乘10、100、1000?，只要把这个小数的小数点向右移动一位、两位、三位?；把一个小数的小数点向右移动了一位、两位、三位?这个小数就扩大了10倍、100倍、1000倍?。一个数（0除外）乘大于1的数时，积比原来的数大，反之就小。

7.小数除以整数的意义：小数除以整数的意义和整数除法的意义相同。 8.小数除以整数的计算方法是按整数进行计算商里的小数点要和被除数的小数点对齐.

9.除数是小数的小数除法的计算方法是先移动除数的小数点，除数的小数点向右移动几位（就是先把除数变成整数），被除数的小数点也向右移动几位（如果数位不够时用0来补足），然后按除数是证书的小数除法进行计算。

10.一个小数除以10、100、1000?，只要把这个小数的小数点向左移动一位、两位、三位?；把一个小数的小数点向左移动了一位、两位、三位?这个小数就缩小了10倍、100倍、1000倍?。

11.被除数不变，除数扩大（或缩小）几倍，商就随着缩小（或扩大）相同的倍数；

除数不变，被除数扩大（或缩小）几倍，商就随着扩大（或缩小）相同的倍数。

被除数和除数同时乘（或除以）相同的数（0除外），商不变。——商不变的规律。

var cpro_psid ="u2572954"; var cpro_pswidth =966; var cpro_psheight =120;

12.小数乘法和小数除法一般用四舍五入法保留小数，有时可根据实际情况选择用“进一法”和“去尾法”保留整数.

13.有限小数：一个小数的小数数位是有限的小数叫做有限小数；小数数位是无限的叫做无限小数。

14.循环小数：一个小数的小数部分是一个数字或者几个数字不断的依次重复出现这样的小树叫做循环小数；这些依次出现的数字叫做这些小数的循环节。循环节的表示方法是如果是一个数字的循环小数就在这个数字上点一个圆点表示他的循环节，是2个数字循环的在这2个数字上点上圆点，3个或3个以上数字循环的只在循环节开始的一位和结束的一位上点上圆点。

15.循环小数的保留时用四舍五入法去近似值。

16.小数混合运算的计算方法和整数混合运算的方法相同。第六单元：统计表和统计图

条形统计图能直接看出数量的多少。

第七单元解决问题的策略（一一列举和图示法） k1.长方形的长＋宽＝长方形周长的一半

2.当长方形的周长不变时，长与宽长度相差的越大，这个长方形的面积就越小；反之，长与宽长度相差的越小，这个长方形的面积就越大。

3.当长方形的面积不变时，长与宽长度相差的越大，这个长方形的周长就越长；反之，长与宽长度相差的越小，这个长方形的周长就越短。第八单元：用字母表示数

1. 用字母表示数的意义是简明易记、方便运用。

2. 在数字和字母、以及字母和字母之间的乘号可以写作·表示；也可以省略不写，但是省略乘号时数字一定要写在字母的前面。例如5×a=5·a=5a x×y×7=7xy

3. 最需要注意的是用字母不仅能表示数还表示了两个数量之间的某种关系。

4. 求代数式的值

例1. 先写出公式，再把数值代入公式计算

1. 一个平行四边形，底5cm,高2.4cm.求它的面积（1） s=ah÷2 （2） s=ah÷2